Rectified 8-orthoplex
8-orthoplex |
Rectified 8-orthoplex |
Birectified 8-orthoplex |
Trirectified 8-orthoplex |
Trirectified 8-cube |
Birectified 8-cube |
Rectified 8-cube |
8-cube |
| Orthogonal projections in A8 Coxeter plane | |||
|---|---|---|---|
In eight-dimensional geometry, a rectified 8-orthoplex is a convex uniform 8-polytope, being a rectification of the regular 8-orthoplex.
There are unique 8 degrees of rectifications, the zeroth being the 8-orthoplex, and the 7th and last being the 8-cube. Vertices of the rectified 8-orthoplex are located at the edge-centers of the 8-orthoplex. Vertices of the birectified 8-orthoplex are located in the triangular face centers of the 8-orthoplex. Vertices of the trirectified 8-orthoplex are located in the tetrahedral cell centers of the 8-orthoplex.
Contents |
Rectified 8-orthoplex
| Rectified octacross | |
|---|---|
| Type | uniform 8-polytope |
| Schläfli symbol | t1{3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagrams | |
| 7-faces | 272 |
| 6-faces | 3072 |
| 5-faces | 8960 |
| 4-faces | 12544 |
| Cells | 10080 |
| Faces | 4928 |
| Edges | 1344 |
| Vertices | 112 |
| Vertex figure | 6-orthoplex prism |
| Petrie polygon | hexakaidecagon |
| Coxeter groups | C8, [4,36] D8, [35,1,1] |
| Properties | convex |
The rectified 8-orthoplex has 112 vertices. These represent the root vectors of the simple Lie group D8. When combined with the 16 vertices of the 8-orthoplex, these vertices represent the 128 root vectors of the B8 and C8 simple Lie groups.
Related polytopes
The rectified octacross is the vertex figure for the demiocteractic honeycomb.
- or
Alternate names
- rectified octacross
- rectified diacosipentacontahexazetton (Acronym: rek) (Jonathan Bowers)[1]
Construction
There are two Coxeter groups associated with the rectified octacross, one with the C8 or [4,36] Coxeter group, and a lower symmetry with two copies of heptcross facets, alternating, with the D8 or [35,1,1] Coxeter group.
Images
| B8 | B7 | ||||
|---|---|---|---|---|---|
| [16] | [14] | ||||
| B6 | B5 | ||||
| [12] | [10] | ||||
| B4 | B3 | B2 | |||
| [8] | [6] | [4] | |||
| A7 | A5 | A3 | |||
| [8] | [6] | [4] | |||
Cartesian coordinates
Cartesian coordinates for the vertices of a rectified octacross, centered at the origin, edge length 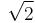 are all permutations of:
are all permutations of:
- (±1,±1,0,0,0,0,0,0)
Birectified 8-orthoplex
| Birectified 8-orthoplex | |
|---|---|
| Type | uniform 8-polytope |
| Schläfli symbol | t2{3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagrams | |
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure | {3,3,3,4}x{3} |
| Coxeter groups | C8, [3,3,3,3,3,3,4] D8, [35,1,1] |
| Properties | convex |
Alternate names
- birectified octacross
- birectified diacosipentacontahexazetton (Acronym: bark) (Jonathan Bowers)[2]
Images
| B8 | B7 | ||||
|---|---|---|---|---|---|
| [16] | [14] | ||||
| B6 | B5 | ||||
| [12] | [10] | ||||
| B4 | B3 | B2 | |||
| [8] | [6] | [4] | |||
| A7 | A5 | A3 | |||
| [8] | [6] | [4] | |||
Trirectified 8-orthoplex
| Trirectified octacross | |
|---|---|
| Type | uniform 8-polytope |
| Schläfli symbol | t3{3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagrams | |
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure | {3,3,4}x{3,3} |
| Coxeter groups | C8, [3,3,3,3,3,3,4] D8, [35,1,1] |
| Properties | convex |
Alternate names
- trirectified octacross
- trirectified diacosipentacontahexazetton (Acronym: tark) (Jonathan Bowers)[3]
Images
| B8 | B7 | ||||
|---|---|---|---|---|---|
| [16] | [14] | ||||
| B6 | B5 | ||||
| [12] | [10] | ||||
| B4 | B3 | B2 | |||
| [8] | [6] | [4] | |||
| A7 | A5 | A3 | |||
| [8] | [6] | [4] | |||
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Richard Klitzing, 8D, uniform polytopes (polyzetta) o3x3o3o3o3o3o4o - rek, o3o3x3o3o3o3o4o - bark, o3o3o3x3o3o3o4o - tark
External links
- Olshevsky, George, Cross polytope at Glossary for Hyperspace.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary